In our program, we will be drawing the same cube from this lesson, except that all of the faces will be transparent. Our program will look like this:

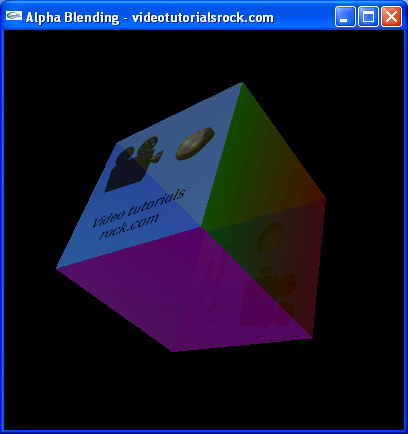
A transparent face has a particular amount of opacity, known as its alpha value. Our faces have an alpha value of 0.6, indicating that they are 60% opaque and 40% transparent. The alpha value is actually considered to be a component of the color of each face. The magenta face, for example, has a color of (1, 0, 1, 0.6).

In order to draw the cube, we draw the faces from back to front. Whenever we draw a face, OpenGL will go through all of the pixels on the face and average them with the pixels that are already there. So when we draw the face that is farthest back, for each pixel, we'll take 60% of that pixel and add 40% of the pixel that's already there, which happens to be black. In other words, the red component of the resulting pixel, for example, will be 0.4 times the red component of the black pixel already there plus 0.6 times the red component of the pixel we're drawing on top.

In earlier programs, the order in which we drew the faces didn't matter. But in this case, it's important to draw them from back to front. This simulates real-world transparency, as light must travel through objects in order from back to front before reaching your eye.

There's actually a clever technique called backface culling that allows us to make transparent objects without carefully sorting the faces. I'll cover that technique in a later lesson. For now, just know that it's out there.

Let's take a look at the code that makes it all happen.

const float PI = 3.1415926535f;
const float BOX_SIZE = 7.0f; //The length of each side of the cube
const float ALPHA = 0.6f; //The opacity of each face of the cube

We start with a few constants: pi, the length of each side of the cube, and the alpha value for each face of the cube.

//Three perpendicular vectors for a face of the cube.  out indicates the
//direction that the face is from the center of the cube.
struct Face {
    Vec3f up;
    Vec3f right;
    Vec3f out;
};

Here, we have a structure that we'll use to store where each face is. We're going to specify the coordinates of each vertex of each face directly rather than using glRotatef to figure them out for us. This is because we need to know the positions of all of the faces, so that we can sort them from back to front.

For each face, we store three perpendicular vectors with magnitude 1. We have the vector out, which points outward from the face. It is the same as the normal vector. We can use it to figure out the center of the face; the center is located at out * BOX_SIZE / 2. up and right are vectors indicating two sides of the face.

//Represents a cube.
struct Cube {
    Face top;
    Face bottom;
    Face left;
    Face right;
    Face front;
    Face back;
};

This structure stores all of the faces of the cube.

//Rotates the vector by the indicated number of degrees about the specified axis
Vec3f rotate(Vec3f v, Vec3f axis, float degrees) {
    axis = axis.normalize();
    float radians = degrees * PI / 180;
    float s = sin(radians);
    float c = cos(radians);
    return v * c + axis * axis.dot(v) * (1 - c) + v.cross(axis) * s;
}

This function rotates a vector a certain number of degrees about a particular axis. I found the formula for this online at MathWorld.

//Rotates the face by the indicated number of degrees about the specified axis
void rotate(Face &face, Vec3f axis, float degrees) {
    face.up = rotate(face.up, axis, degrees);
    face.right = rotate(face.right, axis, degrees);
    face.out = rotate(face.out, axis, degrees);
}

This rotate function rotates a particular face. To do that, we just have to rotate the face's up, right, and out vectors.

//Rotates the cube by the indicated number of degrees about the specified axis
void rotate(Cube &cube, Vec3f axis, float degrees) {
    rotate(cube.top, axis, degrees);
    rotate(cube.bottom, axis, degrees);
    rotate(cube.left, axis, degrees);
    rotate(cube.right, axis, degrees);
    rotate(cube.front, axis, degrees);
    rotate(cube.back, axis, degrees);
}

This rotate function rotates a cube by rotating each of its faces.

//Initializes the up, right, and out vectors for the six faces of the cube.
void initCube(Cube &cube) {
    cube.top.up = Vec3f(0, 0, -1);
    cube.top.right = Vec3f(1, 0, 0);
    cube.top.out = Vec3f(0, 1, 0);
    
    cube.bottom.up = Vec3f(0, 0, 1);
    cube.bottom.right = Vec3f(1, 0, 0);
    cube.bottom.out = Vec3f(0, -1, 0);
    
    cube.left.up = Vec3f(0, 0, -1);
    cube.left.right = Vec3f(0, 1, 0);
    cube.left.out = Vec3f(-1, 0, 0);
    
    cube.right.up = Vec3f(0, -1, 0);
    cube.right.right = Vec3f(0, 0, 1);
    cube.right.out = Vec3f(1, 0, 0);
    
    cube.front.up = Vec3f(0, 1, 0);
    cube.front.right = Vec3f(1, 0, 0);
    cube.front.out = Vec3f(0, 0, 1);
    
    cube.back.up = Vec3f(1, 0, 0);
    cube.back.right = Vec3f(0, 1, 0);
    cube.back.out = Vec3f(0, 0, -1);
}

The initCube function initializes the up, right, and out vectors of each of the faces of a cube.

//Returns whether face1 is in back of face2.
bool compareFaces(Face* face1, Face* face2) {
    return face1->out[2] < face2->out[2];
}

We'll use the compareFaces function to order the faces from back to front. The function returns whether face1 is in back of face2. It does this just by comparing the z components of the faces' out vectors, which basically compares the z coordinates of the centers of the faces.

In general, we can't necessarily sort the faces of an object by the z coordinates of the centers of their faces. That's because each pixel in a given face has a different z coordinate. The z coordinate of the center isn't necessarily important. However, in the case of this cube, comparing the z coordinates of the centers of the faces happens to work, which makes our life easier.

//Stores the four vertices of the face in the array "vs".
void faceVertices(Face &face, Vec3f* vs) {
    vs[0] = BOX_SIZE / 2 * (face.out - face.right - face.up);
    vs[1] = BOX_SIZE / 2 * (face.out - face.right + face.up);
    vs[2] = BOX_SIZE / 2 * (face.out + face.right + face.up);
    vs[3] = BOX_SIZE / 2 * (face.out + face.right - face.up);
}

The faceVertices function figures out the four vertices of the quadrilateral for a face and stores them in a vs array.

void drawTopFace(Face &face) {
    Vec3f vs[4];
    faceVertices(face, vs);
    
    glDisable(GL_TEXTURE_2D);
    glBegin(GL_QUADS);
    
    glColor4f(1.0f, 1.0f, 0.0f, ALPHA);
    glNormal3f(face.out[0], face.out[1], face.out[2]);
    glVertex3f(vs[0][0], vs[0][1], vs[0][2]);
    glVertex3f(vs[1][0], vs[1][1], vs[1][2]);
    glVertex3f(vs[2][0], vs[2][1], vs[2][2]);
    glVertex3f(vs[3][0], vs[3][1], vs[3][2]);
    
    glEnd();
}

The drawTopFace function takes care of drawing the top face of the cube. It first calls faceVertices to figure out where to draw the face. Then, it draws the face.

The call to glColor4f is new. It specifies the color of the face using red, green, blue, and alpha components, which we'll want to do to make the object look transparent.

void drawBottomFace(Face &face) {
    //...
}

void drawLeftFace(Face &face) {
    //...
}

void drawRightFace(Face &face) {
    //...
}

void drawFrontFace(Face &face) {
    //...
}

void drawBackFace(Face &face) {
    //...
    glColor4f(1.0f, 1.0f, 1.0f, ALPHA);
    //...
}

We also have separate functions for drawing the bottom, left, right, front, and back faces. We need separate functions in order to have them be different colors, or use color blending, or use textures.

The back face is a textured face. You'll notice that calling glColor4f allows us to make even textured faces transparent.

//Draws the indicated face on the specified cube.
void drawFace(Face* face, Cube &cube, GLuint textureId) {
    if (face == &(cube.top)) {
        drawTopFace(cube.top);
    }
    else if (face == &(cube.bottom)) {
        drawBottomFace(cube.bottom);
    }
    else if (face == &(cube.left)) {
        drawLeftFace(cube.left);
    }
    else if (face == &(cube.right)) {
        drawRightFace(cube.right);
    }
    else if (face == &(cube.front)) {
        drawFrontFace(cube.front, textureId);
    }
    else {
        drawBackFace(cube.back, textureId);
    }
}

The drawFace function takes a face, figures out whether it is the top, bottom, left, right, front, or back face, and calls the appropriate draw function.

void initRendering() {
    //...
    glEnable(GL_BLEND); //Enable alpha blending
    glBlendFunc(GL_SRC_ALPHA, GL_ONE_MINUS_SRC_ALPHA); //Set the blend function
    //...
}

We have a couple of new calls in initRendering. First, we call glEnable(GL_BLEND) to enable alpha blending.

I'd mentioned that when we draw a pixel for a particular face, in this program, we take 60% of that pixel and 40% of the pixel already there. Well, actually, you can use all kinds of weird functions to figure out the new pixel value. But for normal transparency, you'll want to use the function I mentioned, so we'll just call glBlendFunc(GL_SRC_ALPHA, GL_ONE_MINUS_SRC_ALPHA).

void drawScene() {
    //...
    vector<Face*> faces;
    faces.push_back(&(_cube.top));
    faces.push_back(&(_cube.bottom));
    faces.push_back(&(_cube.left));
    faces.push_back(&(_cube.right));
    faces.push_back(&(_cube.front));
    faces.push_back(&(_cube.back));
    
    //Sort the faces from back to front
    sort(faces.begin(), faces.end(), compareFaces);

When we draw the cube, the first thing we have to do is sort the faces from back to front. We put all of the faces into a faces vector and use the C++ sort function to sort it from back to front. The sort function is available by using #include <algorithm>. The first two arguments are faces.begin() and faces.end(), and the last argument is the comparison function that determines the order in which we'll sort the faces. In this case, we want to sort the faces from back to front, so we use the compareFaces function we saw earlier. The sort function will rearrange the elements of the faces vector so that they're ordered from back to front.

    for(unsigned int i = 0; i < faces.size(); i++) {
        drawFace(faces[i], _cube, _textureId);
    }
    //...
}

Now, we draw the faces in the sorted order.

void update(int value) {
    rotate(_cube, Vec3f(1, 1, 0), 1);
    //...
}

The update function rotates the cube.

int main(int argc, char** argv) {
    //...
    initCube(_cube);
    //...
}

In our main function, we have a call to our initCube function.

That's our program. It shows how to make transparent-looking objects in OpenGL.

Next is "Lesson 13: Particle Systems".