One common feature in games and other 3D programs is the presence of a 3D terrain. In this lesson, we will be making the following terrain:

The question is, how do we represent a terrain? The most straightforward approach, and, as it turns out, one of the best approaches, is to make a 2D grid in the x-z plane and store the height of the terrain at each grid point. This doesn't let us make every terrain; for example, we can't have a purely vertical wall or a wall that is slanted "backwards". But still, we can do a lot.

We could hard code every height into the program itself. But it's better to store the heights in a separate file. The most straightforward type of file we can use is a grayscale image, where white represents the maximum allowable height and black represents the minimum allowable height. Such an image file is called a "heightmap". This also turns out to be a good idea. For one, it allows us to see what our terrain looks like, even without rendering it in 3D. Below is a zoomed-in version of the heightmap for our program.

There are some tools out there for making and manipulating heightmaps, although I'm not too familiar with them. How did I make this heightmap, then? That's my secret.

Let's see how our program loads and displays the terrain. You'll notice that at the top, we have #include "vec3f.h". This includes a special vector class I wrote called "Vec3f", a vector of three floats. It does everything you'd expect vectors to do. You can add and subtract using + and -, multiply and divide using * and /, get or set the components using vec[0], vec[1], and vec[2], and do some other stuff. You can even cout a Vec3f. You can see everything that you can do with a Vec3f by looking at vec3f.h. We'll use the Vec3f class to store normal vectors.

//Represents a terrain, by storing a set of heights and normals at 2D locations
class Terrain {
    private:
        int w; //Width
        int l; //Length
        float** hs; //Heights
        Vec3f** normals;
        bool computedNormals; //Whether normals is up-to-date

Here's our terrain class. It stores a width and length, indicating the number of grid points in the x and z directions respectively. It stores all of the heights and the normals at each point using two-dimensional arrays. Finally, it has a bool that tells us whether the normals array actually has the correct normals. We'll want to first set all of the heights and then compute all of the normals at once, so the normals may not yet have been computed.

        Terrain(int w2, int l2) {
            w = w2;
            l = l2;
            
            hs = new float*[l];
            for(int i = 0; i < l; i++) {
                hs[i] = new float[w];
            }
            
            normals = new Vec3f*[l];
            for(int i = 0; i < l; i++) {
                normals[i] = new Vec3f[w];
            }
            
            computedNormals = false;
        }

Here's the constructor for the Terrain class. It initializes all of our variables.

        ~Terrain() {
            for(int i = 0; i < l; i++) {
                delete[] hs[i];
            }
            delete[] hs;
            
            for(int i = 0; i < l; i++) {
                delete[] normals[i];
            }
            delete[] normals;
        }

Next is the destructor for the Terrain class. The destructor deletes the two-dimensional arrays hs and normals.

        int width() {
            return w;
        }
        
        int length() {
            return l;
        }

These are methods that return the width and length of the terrain.

        //Sets the height at (x, z) to y
        void setHeight(int x, int z, float y) {
            hs[z][x] = y;
            computedNormals = false;
        }
        
        //Returns the height at (x, z)
        float getHeight(int x, int z) {
            return hs[z][x];
        }

These methods allow us to set and get the height of the terrain at a particular grid point.

        //Computes the normals, if they haven't been computed yet
        void computeNormals() {
            //...
        }

This method computes the normal at each point. We'll come back to it.

        //Returns the normal at (x, z)
        Vec3f getNormal(int x, int z) {
            if (!computedNormals) {
                computeNormals();
            }
            return normals[z][x];
        }
};

Here, we have a method that returns the normal at some point.

//Loads a terrain from a heightmap.  The heights of the terrain range from
//-height / 2 to height / 2.
Terrain* loadTerrain(const char* filename, float height) {
    Image* image = loadBMP(filename);
    Terrain* t = new Terrain(image->width, image->height);
    for(int y = 0; y < image->height; y++) {
        for(int x = 0; x < image->width; x++) {
            unsigned char color =
                (unsigned char)image->pixels[3 * (y * image->width + x)];
            float h = height * ((color / 255.0f) - 0.5f);
            t->setHeight(x, y, h);
        }
    }
    
    delete image;
    t->computeNormals();
    return t;
}

Here's our function for loading a terrain from an image file. First, we call our trusty ol' loadBMP function to load the bitmap from file. Then' we go through the pixels of the array and use them to set the heights of the terrain. A color of 0 corresponds to a height of -height / 2, and a color of 255 corresponds to a height of height / 2. It doesn't matter which color component we use; I used the red component for no particular reason. Then, we delete the image and force the terrain to compute all of the normals.

Now let's skip down to partway into drawScene.

    float scale = 5.0f / max(_terrain->width() - 1, _terrain->length() - 1);
    glScalef(scale, scale, scale);
    glTranslatef(-float(_terrain->width()) / 2,
                 0.0f,
                 -float(_terrain->length()) / 2);

We scale our terrain, so that it is at most 5 units wide and 5 units long. Then, we translate it so it's centered.

    glColor3f(0.3f, 0.9f, 0.0f);
    for(int z = 0; z < _terrain->length() - 1; z++) {
        //Makes OpenGL draw a triangle at every three consecutive vertices
        glBegin(GL_TRIANGLE_STRIP);
        for(int x = 0; x < _terrain->width(); x++) {
            Vec3f normal = _terrain->getNormal(x, z);
            glNormal3f(normal[0], normal[1], normal[2]);
            glVertex3f(x, _terrain->getHeight(x, z), z);
            normal = _terrain->getNormal(x, z + 1);
            glNormal3f(normal[0], normal[1], normal[2]);
            glVertex3f(x, _terrain->getHeight(x, z + 1), z + 1);
        }
        glEnd();
    }

Here, we draw the terrain. GL_TRIANGLE_STRIP is new. It makes OpenGL draw a triangle at every three consecutive vertices that you indicate. If your vertices are v1, v2, v3, ..., then OpenGL will draw the triangles (v1, v2, v3), (v2, v3, v4), (v3, v4, v5), .... To draw the terrain, for each z, we do a triangle strip with vertices (0, h1, z), (0, h2, z + 1), (1, h3, z), (1, h4, z + 1), (2, h5, z), (2, h6, z + 1), .... Using triangle strips is not only more convenient than using triangles; it's faster, as there are fewer 3D vertices to send to the graphics card. So, our terrain is drawn as shown below:

The way we draw the terrain, each cell in the x-z grid is carved up into two triangles, using the diagonal going out and to the right. We could have used the other diagonal to carve each cell, but it doesn't matter too much if our terrain is "smooth enough". We also could have used GL_QUADS instead, but that's not such a good idea when the four vertices aren't in the same plane.

int main(int argc, char** argv) {
    //...
    _terrain = loadTerrain("heightmap.bmp", 20);
    //...
}

In our main function, we call loadTerrain to load the 3D terrain.

Now let's go back and see how we computed our normals.

        //Computes the normals, if they haven't been computed yet
        void computeNormals() {
            if (computedNormals) {
                return;
            }
            
            Vec3f** normals2 = new Vec3f*[l];
            for(int i = 0; i < l; i++) {
                normals2[i] = new Vec3f[w];
            }
            
            for(int z = 0; z < l; z++) {
                for(int x = 0; x < w; x++) {
                    Vec3f sum(0.0f, 0.0f, 0.0f);
                    
                    Vec3f out;
                    if (z > 0) {
                        out = Vec3f(0.0f, hs[z - 1][x] - hs[z][x], -1.0f);
                    }
                    Vec3f in;
                    if (z < l - 1) {
                        in = Vec3f(0.0f, hs[z + 1][x] - hs[z][x], 1.0f);
                    }
                    Vec3f left;
                    if (x > 0) {
                        left = Vec3f(-1.0f, hs[z][x - 1] - hs[z][x], 0.0f);
                    }
                    Vec3f right;
                    if (x < w - 1) {
                        right = Vec3f(1.0f, hs[z][x + 1] - hs[z][x], 0.0f);
                    }
                    
                    if (x > 0 && z > 0) {
                        sum += out.cross(left).normalize();
                    }
                    if (x > 0 && z < l - 1) {
                        sum += left.cross(in).normalize();
                    }
                    if (x < w - 1 && z < l - 1) {
                        sum += in.cross(right).normalize();
                    }
                    if (x < w - 1 && z > 0) {
                        sum += right.cross(out).normalize();
                    }
                    
                    normals2[z][x] = sum;
                }
            }

First we'll compute approximate normals, and store them in the variable normals2. One way to estimate a normal at a given point is to take the vector that is perpendicular to a triangle with vertices at the point and at two points adjacent to it. For example, we could take the triangle with vertices at the point, the point immediately right of it, and the point immediately outward with respect to it, and take a vector perpendicular to that.

To find the vector perpendicular to a triangle, we take the cross product of two of its edges. We compute the four edges in, out, left, and right for each point. Then, we take the cross product of a pair of edges to determine the vector perpendicular to a triangle. We do this for each of the four triangles "adjacent" to the point and take the average of the four vectors (which is just proportional to the sum).

What exactly does an average of four normal vectors mean, geometrically? Absolutely nothing. It's just a way I came up with to approximate the normals. The cardinal rule of computer graphics is to do what looks right. So let's see if this weird averaging will work out in the end.

Note that we have to use a bunch of if statements for points that are at the edges, since they may have fewer than four "adjacent" triangles.

Okay, so we computed a bunch of normals. But it would be nice to "smooth" them out, so that each normal is more similar to adjacent normals. This way, the lighting in our 3D scene will look more smooth. This is particularly important because the heighmap only uses 64 different heights, so each height has a limited amount of precision, making the lighting look rough. To motivate us, here's a side-by-side comparison of our scene with unsmoothed and smoothed normals:

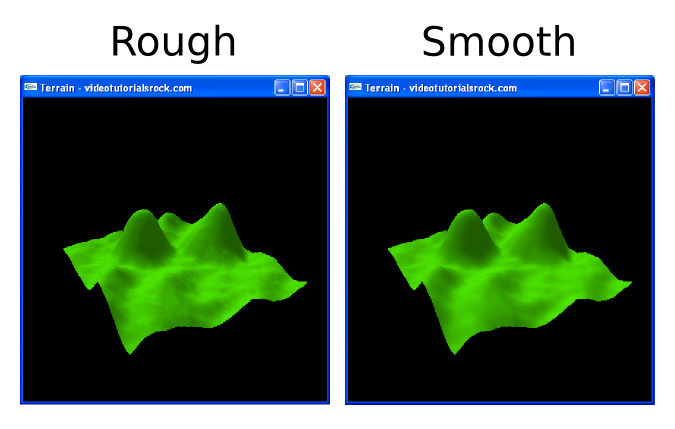
How exactly are we going to smooth the normals? For each normal, let's average in a little bit of the surrounding normals.

            const float FALLOUT_RATIO = 0.5f;
            for(int z = 0; z < l; z++) {
                for(int x = 0; x < w; x++) {
                    Vec3f sum = normals2[z][x];
                    
                    if (x > 0) {
                        sum += normals2[z][x - 1] * FALLOUT_RATIO;
                    }
                    if (x < w - 1) {
                        sum += normals2[z][x + 1] * FALLOUT_RATIO;
                    }
                    if (z > 0) {
                        sum += normals2[z - 1][x] * FALLOUT_RATIO;
                    }
                    if (z < 0) {
                        sum += normals2[z + 1][x];
                    }
                    
                    if (sum.magnitude() == 0) {
                        sum = Vec3f(0.0f, 1.0f, 0.0f);
                    }
                    normals[z][x] = sum;
                }
            }

So, at each normal, we point, we take a weighted average of the "rough" normal at the point and the "rough" normal at the adjacent points. Each adjacent normal gets a weight of 0.5, and the normal at the point gets a weight of 1. Again, this average has no real meaning, but it still makes the scene look good. Note that we set the normal to some arbitrary vector if the average turns out to be the zero vector. This is because we can't use the zero vector, as it's impossible to normalize, but we have to use something.

The lighting in our scene looks pretty good. Mission accomplished. Now you know how to make a nice-looking 3D terrain.

Next is "Lesson 8: Drawing Text".